色五月第二季 联邦学习中的诡秘保护本事
连年来, 大数据驱动的东说念主工智能迸发出巨大后劲, 在金融、医疗、城市筹划、自动驾驶等多个领域完成了大范围复杂任务学习. 机器学习看成东说念主工智能的中枢本事, 其性能和诡秘性也广受存眷. 传统的机器学习需要由处事商汇注用户的数据后聚合锻练, 然而用户的数据与用户个体紧密关系, 可能顺利包含敏锐信息, 如个东说念主年齿、种族、患病信息等; 也可能转折佩带隐含的敏锐信息, 如个东说念主网页浏览纪录、内容偏好所隐含的用户政事倾向. 要是这些敏锐信息在汇注过程中被处事商涌现或者运用, 将顺利胁迫用户的东说念主身安全、个东说念主名誉和财产安全. 即常处事商莫得顺利公开用户数据, 聚合锻练后发布的模子也可能因为受到诡秘袭击而涌现参与锻练的数据. 跟着诡秘问题受到的存眷进程日益提高, 用户分享数据的意愿越来越低. 与之矛盾的是, 东说念主工智能本事却必须依靠普遍数据汇注和和会, 要是不成获取齐备丰富的信息来锻练模子并发展本事色五月第二季, 东说念主工智能应用的发展将受到严重完了.
在数据孤岛好意思瞻念与数据和会需求的矛盾迂缓突显的布景下, 联邦学习(federated learning, FL)应时而生. 2017年, Google公司初度建议了联邦学习的成见[1], 这是一种由多个数据持有方(如手机、物联网斥地, 或者金融、医疗机构等)协同锻练模子而不分享数据, 仅在中间阶段交换锻练参数的学习机制. 瞎想气象下, 联邦学习得到的分享模子与数据聚合在中心处事器上锻练所得模子比较, 效力邻近或更好[2]. 由此, 企业莽撞通过正当且高效的形状和会数据索求信息, 个东说念主或其他持出奇据的机构依然莽撞在享受企业提供的东说念主工智能处事的同期, 保出奇据的戒指权.
尽管联邦学习幸免了将数据顺利线路给第三方, 对于数据诡秘有自然的保护作用, 然而其中依然存在普遍诡秘涌现的风险.
● 最初, 联邦学习需要交换中间参数协同锻练, 可能涌现诡秘. 与聚合式学习不同, 联邦学习锻练过程需要交换普遍中间参数, 其所佩带原始数据会线路在统统参与锻练的脚色眼前, 带来涌现的风险. 举例, 已有研究标明, 不错通过梯度还原部分原始数据[3], 或笔据中间参数推断掌持的纪录内容是否来自某个特定参与者[4].
● 其次, 不可靠的参与方加重了诡秘涌现的风险. 联邦学习中, 各个参与方由于地舆、斥地等条目不同, 通讯内容的灵验性和身份的信得过性都难以证据, 因此一朝出现不可靠的参与方袭击, 极易涌现诡秘.举例, 半赤诚的参与方莽撞笔据正当获取的中间参数推断出其他参与方的标签或数据; 而坏心的参与方更进一步, 莽撞通过上传悉心联想的无益信息不异其他参与方线路更多自身数据, 或者不盲从诡秘条约进而影响全局的诡秘性.
● 此外, 锻练完成的模子也靠近着诡秘涌现的风险. 即便联邦学习的过程中参数莫得涌现, 顺利发布锻练所得的模子依然存在极大风险. 这种风险来自机器学习自身的脆弱性. 在锻练中, 模子提高准确性依赖于对数据样本的礼貌挖掘. 然而研究者[4]扎眼到, 追求模子在锻练样本上的准确度, 可能导致模子的参数乃至结构“记取”锻练样本的细节, 使得模子佩带锻练集的敏锐信息. 笔据这一性格, 袭击者不错通过反复查询模子的预测接口来推测某笔纪录是否存在于锻练集、推测模子的具体参数, 而笔据模子发布的参数莽撞进一步推测锻练集成员或锻练集具体样本.
由此可见, 不加保护的进行联邦学习, 锻练中触及的浩荡参与者的数据都将靠近涌现的风险. 而数据一朝涌现, 不仅诡秘涌现者靠近严重赔本, 参与者间互确信任合作的结伴锻练模式也将难合计继.
不断联邦学习信息涌现问题山水相连. 关联词, 联邦学习中数据漫衍复杂、应用场景丰富且需要屡次数据交换, 这些成分为诡秘保护带来一系列挑战.
● 第一, 联邦学习的锻练场景种种且需求复杂, 现存的诡秘保护方法无法通用. 已有的聚合式机器学习诡秘保护研究以中心处事器赤诚为前提, 仅有计划模子发布后可能受到的袭击, 莫得针对里面袭击者的不断决策. 而且现存算法大多针对单一的聚合式锻练场景, 莫得有计划多个参与方、多种架构、多种数据漫衍形状下的数据交换和模子协同锻练的情况. 因此, 联想得当不同场景和不同需求的诡秘保护算法, 同期抵御外部和里面袭击, 是联邦学习诡秘保护的遑急挑战.
● 第二, 联邦学习中参与方的委果进程低, 潜在的袭击角度多, 对诡秘保护算法的鲁棒性要求更高. 这里, 鲁棒性指模子容忍坏心袭击安谧运行的技艺. 联邦学习中, 参与者一朝发起袭击, 莽撞不雅察到更多的中间参数, 以致莽撞删改参数影响锻练过程, 诡秘驻扎的难度远高于外部出现的袭击. 而参与者之间要是共谋, 可能获取更多敏锐信息. 因此, 提高诡秘保护算法的鲁棒性, 减少诡秘算法中对参与者的委果进程的假设, 是联邦学习诡秘保护靠近的难题.
● 第三, 联邦学习自身通讯不安谧, 模子筹划代价高, 因而对诡秘保护机制的通讯量和复杂度要求严格. 履行场景下的联邦学习所靠近的复杂松散的汇注结构导致末端通讯不安谧, 在此基础上的诡秘保护算法难以简化. 而复杂的诡秘保护算法将带来更高的筹划量、更大通讯代价, 进一步制约联邦学习的锻练效力. 研究高效力、轻量级的联邦学习诡秘保护算法, 镌汰额外支出, 是联邦学习诡秘保护必须面对的挑战.
● 第四, 联邦学习中参数维度高、数据漫衍不均, 难以在提供诡秘保护的同期保持模子的可用性. 联邦学习中间参数的维度与模子结构和输入数据维度关系, 参数维度时时极高, 形成了极大的诡秘支出.此外, 联邦学习的用户数目不定且数据集大小不一, 如安在均衡不同数据集的同期保护诡秘, 亦然一个巨大挑战.
说七说八, 愈加精致的诡秘计策联想、愈加精准的诡秘预算分拨、愈加得当数据交换的诡秘条约构建, 是联邦学习诡秘保护进一步发展必须面对的议题. 而明确现存的诡秘问题和保护技能, 是本事发展的基础. 联邦学习的基础——机器学习的诡秘袭击和驻扎还是被充分调研[5]. 机器学习靠近的外部袭击同样胁迫着联邦学习的发布模子, 然而机器学习的诡秘保护技能却远远不及合计联邦学习提供保护. 这是由于联邦学习同期靠近着传统的外部袭击和其特有的里面袭击, 因此联邦学习的诡秘保护决策必须同期为里面锻练过程和外部模子发布提供双重保护.
另外, 已有学者调研了联邦学习诡秘保护的近况, 但由于念念路与本文不同, 侧重的方法和文件也不不异. Lyv等东说念主[6]和Wang等东说念主[7]春联邦学习可能受到的袭击作了详备的诠释, 然而在安全袭击和诡秘袭击的区分上莫得进一方法研. 本雅致确两种袭击的成见范围: 以窃取数据、龙套模子诡秘性和奥密性为宗旨的袭击为诡秘袭击, 以插手模子锻练完了、龙套模子可用性和齐备性的袭击为安全袭击. 此外, 本文还依据现存的诡秘袭击本事的旨趣归纳了主要计策分类. 现存文件[7−10]均从本事或锻练阶段的角度分析了现时的联邦学习诡秘保护算法, 而本文笔据联邦学习自身性格分析其特有的诡秘涌现内容和涌现位置, 从诡秘保护的对象的角度启航成立分类框架, 并归纳每个类别中主要的保护机制, 进而分析选拔不同本事的算法的共性并探究机制自身的上风和不及. 进一局势, 本文成立了袭击计策与保护机制之间的磋议, 并在此基础上尝试为联邦学习诡秘保护的发展建议建议.
本文第1节先容联邦学习的架构和类型, 以及相应场景下的锻练形状. 第2节分析联邦学习面对的诡秘涌现风险开端, 总结具体的袭击计策. 第3节先容多种诡秘保护本事旨趣, 并将其归纳为信息迂缓、过程加密两种诡秘保护机制. 第4节调研诡秘保护本事在联邦学习中的应用, 涵盖土产货保护、中心保护、中心与土产货结合这3种保护计策, 并对每种计策张开愈加详备的诠释. 第5节计划现存不及并预计昔时场合.
1 联邦学习联邦学习的一般界说为[11]: N个参与方{F1, …, FN}各自持有锻练集{D1, …, DN}. 联邦学习中, 各个参与方在不将土产货数据Di线路给第三方的情况下, 协调锻练模子MFED. 为了给联邦学习模子一个斟酌表率, 设传统的聚合式机器学习将各个数据集汇注结并为D=D1∪…∪DN以锻练模子MSUM. 令VFED为联邦学习模子MFED精度(performance), VSUM为传统机器学习模子MSUM精度. 存在非负实数δ, 使得:
$\left| {{V_{FED}} - {V_{SUM}}} \right| < \delta , $则称此联邦学习模子具有δ的精度赔本. 可见, 使各个数据集留在土产货协同锻练所得模子的精度, 瞎想气象下应当接近于将数据集聚合后锻练所得模子的精度.
区别于传统的漫衍式机器学习, 联邦学习具有如下特质.
(1) 各个参与方的锻练集非孤苦同漫衍. 各个参与方仅掌持局部信息, 其漫衍与全局不一定不异; 各个参与方仅掌持统统这个词数据集的部分属性及标签信息, 且各方之间属性和标签可能不完满叠加.
(2) 各个参与方的锻练集大小可能抵挡衡. 某些参与方可能由于其范围、影响力等成分掌持更多数据.
(3) 参与方数目不定. 参与者数目可能很少, 举例只好几个企业交换数据集; 也可能极多, 如锻练触及比比皆是的App使用者.
(4) 通讯受限. 与漫衍式比较, 联邦学习的架构更为松散, 参与的斥地可能存在时时掉线、通讯迂缓等情况, 因此联邦学习的通讯代价同样受到极大存眷.
笔据这些特质, 学者为联邦学习联想了不同的架构形状和学习类型.
1.1 联邦学习架构常见的联邦学习架构为客户-处事器. 典型的客户-处事器架构由一个中心处事器和多个持出奇据的客户端构成. 被庸俗选拔的联邦平均FedAvg[1]便是基于客户-处事器架构联想的算法. 在锻练中, 中心处事器将当场驱动化的模子结构和参数分发给客户端, 客户端笔据土产货数据锻练并更新模子后将参数上传. 中心处事器收到各方参数后团聚筹划, 更新模子参数再次下发. 该过程轮回, 直至模子敛迹或锻练停止. 除了常见的模子参数交换之外, 也存在梯度交换、数据特征的镶嵌式暗示交换等形状. 在此架构下, 原始数据不需要传输, 然而土产货中间参数线路给了中心处事器, 全局中间参数则会被每个客户端获取, 数据交换过程中, 巨大的通讯量也会影响锻练效力. 而当参与锻练的客户端数目过多时, 中心处事器的团聚筹划以致可能成为全局锻练效力的瓶颈.
当莫得中心处事器时, 联邦学习选拔另一种常见架构: 端对端的汇注架构[12]. 这种架构仅由持出奇据的末端构成. 参与锻练的末端Fi顺利将锻练参数发送给下一个(或多个)末端Fi+1, 下一个(或多个)末端Fi+1在汇注到的一个(或多个)参数基础上不绝锻练, 直到模子敛迹或者锻练停止. 端对端汇注架构不依赖中心处事器这么的第三方机构, 土产货中间参数顺利在参与方之间传送. 因此需要有计划参与方若何协商使用不异的模子、算法、驱动化参数等基本信息, 协调各方参与锻练的递次.
为了下文中成见融合、表述明晰, 本文将客户-处事器中的处事器称为中心处事器; 将客户-处事器中的客户端和端对端架构中的参与锻练末端统称为末端; 统统参与锻练的处事器、末端统称为参与方. 锻练过程中发送的梯度、模子参数、镶嵌式暗示等, 统称为中间参数. 上述两种典型架构如图 1所示.
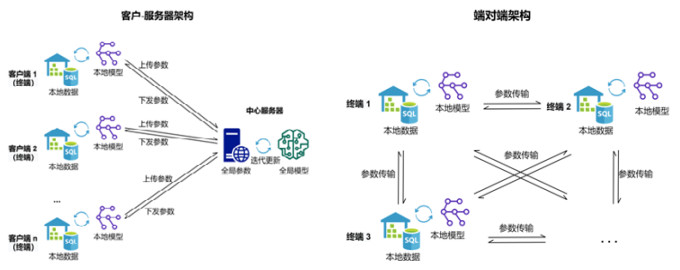图 1 联邦学习中的典型架构
1.2 联邦学习类型
笔据参与方的样本漫衍情况, 联邦学习按照数据的分手情况不错分为3种类型: 横向联邦学习、纵向联邦学习、转移联邦学习. 不同的数据的分手形状需要的锻练形状和中间参数不同, 也为诡秘涌现的风险和保护形状带来影响.
横向联邦学习中, 各个参与方持有的数据特征不异, 但掌持的样本不同. 举例, 几个不同城市的病院可能掌持着不同病东说念主的情况, 然而由于具备相似的医疗技能, 病院获取属性的属性不异. 横向联邦学习中典型的形状之一是第1.1节所刻画的联邦平均算法FedAvg, 包括梯度平均和模子平均两种类型[13], 多由客户-处事器架构完毕. 梯度平均是指末端交换和团聚模子梯度, 而模子平均指团聚模子参数. 在端对端架构中, 各个参与方锻练土产货模子, 通过轮回发送给下一个(或多个)锻练方或者当场传输某个(或多个)末端[14]完毕模子参数的分享.
而纵向联邦学习则针对相背的情形, 即各个参与方持有的数据特征不同, 但掌持的样本不异. 举例, 销毁个城市中的病院和银行都管待过销毁个市民, 保留着该市民的就诊纪录或资金气象. 彰着, 病院和银行获取的数据属性完满不同, 然而所持有的样本ID是叠加的. 纵向联邦学习最初需要参与方对王人不异ID的样本, 然后, 各个参与方在对王人的样本上分别锻练土产货模子并分享参数. 不同架构同样都适用于纵向联邦学习, 但由于数据的纵向漫衍, 参与方之间的依赖进程更高, 模子需要愈加精致地联想. 纵向联邦学习已应用于线性回想[11]、训导树[15]、梯度下落[16]等多种模子上. 以纵向联邦学习线性回想算法[11]为例, 该算法在样本对王人后, 将赔本函数的梯度拆分, 使得两个参与方莽撞使用各自的土产货数据分别筹划梯度的一部分, 而需要共同筹划的部分则通过两边交换参数协同完成. 纵向漫衍的数据之间紧密的关系性, 为纵向学习的效力和容错性带来挑战.
上述两种类型都是比较瞎想的情况, 履行生计中, 大部分参与方所持有的数据, 在特征和样本ID上的叠加都比较少且数据集漫衍抵挡衡. 针对这么的情形, 转移学习被应用到联邦学习中来. 转移学习看成一种灵验的学习念念想, 莽撞将关系领域中的常识转移到方针领域中, 使得各个参与方共同学习得到转移常识. 以两方转移学习为例[17], 假设一方A掌持样本的部分特征和一王人标签, 另一方B掌持部分特征, 两边特征和样本ID之间都有极少叠加. 联邦转移学习最初对王人样本并共同锻练模子, 然后预测B方样本的标签. 为了达到预期效力, 锻练的方针函数包含两个部分: 一部分是笔据已有的标签预测B方样本, 使预测障碍最小化; 另一部分是A与B对王人的样本之间的镶嵌式暗示的区别最小化. 各方笔据方针函数在土产货锻练, 并交换中间参数更新模子, 直至模子敛迹.
现时, 纵向和转移联邦学习的诡秘保护算法研究还不闇练, 且保护形状与横向联邦学习场景近似. 为了表述纯粹, 下文中调研的诡秘保护算法若无很是说明, 即为横向联邦学习场景.
2 联邦学习中的诡秘涌现风险尽管联邦学习不顺利交换数据, 比传统的聚合式机器学习锻练有了更高的诡秘保险, 但联邦学习自身并莫得提供全面充分的诡秘保护, 依然靠近着信息涌现的胁迫. 模子靠近的诡秘涌现风险来自模子锻练自身的脆弱性和袭击者的强劲技艺: 模子锻练过程中, 独特架构和锻练阶段决定了诡秘涌现的位置和时机; 袭击者的脚色和技艺, 决定了诡秘涌现的内容和进程. 而袭击者依据自身性格所遴选的袭击计策, 则进一步影响袭击者的技艺, 从而影响模子诡秘涌现的风险. 理清诡秘涌现的风险, 技艺为联邦学习诡秘驻扎找到总体场合.
2.1 诡秘涌现风险开端为了鄙人文中更好地刻画诡秘袭击, 咱们最初成立联邦学习袭击模子.
● 笔据脚色, 袭击者分为里面和外部: 里面袭击者包括掌持锻练的中间参数况兼参与锻练过程的末端和中心处事器; 而外部袭击者包括掌持模子发布的参数及查询接口但莫得参与锻练过程的模子使用者. 与外部袭击者比较, 里面袭击者掌持模子的更多信息, 袭击技艺更强.
● 笔据委果进程, 袭击者分为半赤诚脚色和坏心脚色: 半赤诚脚色指参与方严格盲从锻练条约和过程, 仅笔据正当获取的信息分析推断, 对于锻练完了莫得影响; 坏心脚色指参与方不盲从条约, 在参与过程中坏心删改数据、注入模块, 不异方针涌现诡秘并影响锻练完了.
● 笔据袭击模式, 袭击分为被迫和主动: 被迫袭击指袭击者仅不雅察或探望模子获取信息; 主动袭击指袭击者删改数据或模子, 参与并影响锻练过程. 需要说明的是, 袭击模式与委果进程并非完满对应. 存在少数主动袭击者莽撞在修改上传参数不异方针涌现诡秘的同期不影响联邦锻练方针, 赤诚正确地完成锻练任务.
● 笔据袭击者常识, 袭击分为白盒袭击和黑盒袭击: 白盒袭击指袭击者掌持模子的关系信息, 包括数据的漫衍和统计信息、模子锻练完成的结构参数或模子锻练过程中的中间参数; 黑盒袭击指袭击者对关系信息一无所知, 仅有苦求查询的权限.
联邦学习包含参数上传、下发、参数传输、模子发布等多个阶段, 其中, 参数上传、下发为客户-处事器架构所特有的阶段, 参数传输为端对端架构所特有的阶段, 模子发布为两种架构都有的阶段. 每个阶段诡秘涌现的位置和内容不同, 胁迫诡秘的袭击者脚色也不不异. 研究联邦学习不同阶段诡秘涌现风险, 有助于为诡秘保护提供明晰的念念路和场合. 诡秘涌现风险开端的对比见表 1.
表 1 诡秘涌现风险开端
在客户-处事器架构下, 锻练分为3个阶段.
● 第1阶段, 土产货(末端)锻练后, 上传土产货参数给中心处事器. 此阶段的潜在袭击者多为中心处事器. 中心处事器笔据汇注的土产货参数莽撞发起重建袭击, 复原方针末端的原始数据; 或者发起属性推断袭击, 推断方针末端的数据中是否含有某些敏锐属性.
● 第2阶段, 中心处事器团聚各个末端的参数处理后, 再次下发全局参数. 此时的潜在袭击者是不委果的末端. 末端莽撞笔据全局中间参数发起袭击重建某个类别样本(generic sample), 或推断某笔纪录的敏锐属性是否存在, 进而笔据锻练集的共同特征推断领有该纪录的个体的情况, 举例锻练集是艾滋病患者基因数据, 要是该个体属于该锻练集, 则一定也患有艾滋病.
● 第3阶段, 模子锻练完成, 由中心处事器发布模子. 一般的发布形状包括顺利将模子部署在用户端, 或提供API探望接口两种. 此时的潜在袭击者是外部使用者. 不委果的外部使用者莽撞笔据模子的参数或模子的预测完了发起推断袭击、重建袭击或参数索求袭击[18−22]. 通过发布的模子推测参与锻练的数据集样本, 或笔据API探望接口推测模子参数, 进而袭击锻练数据.
在端对端架构下, 锻练分为两个阶段:
● 第1阶段, 土产货(末端)锻练后, 将土产货参数传输给下一末端. 袭击者为不委果的接受末端. 末端接受土产货参数后, 同样莽撞发起重建袭击或属性推断袭击, 致使土产货的原始数据涌现.
● 第2阶段, 模子锻练完成后, 末端若发布模子, 则靠近与客户-处事器架构同样的外部袭击; 若仅供里面使用, 则毋庸有计划.
需要说明的是, 联邦学习的诡秘袭击主要由里面参与方发起. 与外部袭击者比较, 里面袭击者具备更强的技艺, 不仅不错在锻练过程中通过顺利获取数据交换中的特征镶嵌式暗示、梯度和模子参数等发起袭击, 还莽撞通过替换样本、更正梯度以致修改赔本函数等形状影响模子的锻练过程, 不异方针末端线路更多诡秘信息, 完成推断袭击和重建袭击. 联邦学习为了协同锻练和分享模子需要更多参与者, 却阑珊与之对应的身份证据机制和诚信保险, 难以驻扎“里面”涌现. 传统的聚合式机器学习诡秘保护莽撞抵御外部袭击, 却莫得抵御里面袭击的技艺. 为了理清联邦学习面对的风险, 本文最初先容外部袭击看成基础, 要点针对其特有的里面诡秘袭击张开分析.
2.2 诡秘袭击计策笔据上述的诡秘涌现风险和袭击者的技艺, 研究者联想了不同的联邦学习架构及阶段下可能的诡秘袭击, 并通过实验展现了这些袭击对敏锐数据的巨大胁迫. 诡秘袭击者包括参与模子锻练的里面脚色和未参与模子锻练仅能战斗发布模子的外部脚色. 袭击者遴选的主要计策有重建袭击和推断袭击: 重建袭击中, 袭击者笔据掌持的中间参数以及模子信息复原部分锻练数据; 推断袭击中, 袭击者笔据中间参数和发布参数推断锻练聚合是否含有特定的纪录. 里面以及外部袭击者选拔上述计策春联邦学习发起诡秘袭击, 获取锻练集的敏锐信息. 其中, 里面诡秘袭击决策的总结参见表 2.
表 2 里面诡秘袭击具体决策
2.2.1 重建袭击
重建袭击(reconstruction attack)指袭击者笔据锻练中间参数、模子的参数或者苦求查询所得输出, 复原参与锻练的数据聚合的信息. 笔据袭击者脚色, 重建袭击分为外部和里面袭击: 外部重建袭击是在模子锻练完成并发布后, 外部使用者发起的袭击; 里面重建袭击则是在模子锻练阶段, 里面参与方发起的袭击.
外部重建袭击中, 袭击者仅能掌持模子的查询完了或模子发布的结构和参数, 因此只可继续试探模子的输出完了, 通过诊治输入数据使输出值向预期场合靠近. Fredrikson等东说念主[20]初度联想了外部袭击者在黑盒情况下发起的模子倒推袭击, 该算法基于模子的输出和一些非敏锐属性复原了病东说念主的基因信息. 袭击者假设样本共有d维特征, 其中, f1到fd−1为非敏锐特征, 在给定非敏锐特征和模子输出时, 最大化敏锐特征fd的后验概率.上述使命仅能推断敏锐属性, Fredrikson等东说念主[21]在随后的使命中联想了白盒情况下的模子倒推袭击. 外部袭击者笔据锻练完成的模子参数锻练深度学习模子, 复原锻练聚合的一王人特征. 该袭击通过保持汇注结构和参数不变, 对输入的当场像素值和当场标签梯度下落. 当模子预测置信度达到最优时, 生成的图片像素与锻练集数据高度近似. Luo等东说念主[32]初度建议了纵向联邦学习中的特征重建袭击. 掌持标签的主动参与方在获取最终模子的预测完了后, 莽撞笔据公式倒推或通过旅途完了重建不掌持标签的被迫参与方的数据特征. 上述算法的袭击者脚色均为外部袭击者, 仅能掌持模子得查询完了或模子发布的结构和参数, 因此只可继续输入数据试探模子的输出完了.
外部袭击以模子输出以及发布的最终参数为依据, 重建统统这个词数据集的泛化样本(generic sample), 难以获取详备的敏锐信息. 此外, 借助灵验的泛化、镌汰输出精度等技能, 即可在很猛进程上抵御这类袭击. 比较之下, 联邦学习的里面重建袭击具有愈加丰富的常识布景, 莽撞以中间参数为依据发起袭击. 中间参数不仅与用户数据紧密关系, 而且在迭代中屡次线路. 里面袭击者莽撞据此重建特定用户的具体敏锐信息. 在主动袭击的情况下, 还莽撞通过修改中间参数、上传无益信息来影响模子的锻练过程, 以致不异诡秘涌现. 具体的里面重建袭击包含两种类型: 类别重建和样本重建.
里面类别重建是重建袭击中的常见类型, 该袭击通过重建某个类别的通用样本模式获取方针类别(target class)中的敏锐信息. 举例, 在锻练图片识别分类器时, 锻练集的一个类别中包含的图片主体是一致的, 则类别重建莽撞复原方针类别中主体的共性信息. Hitaj等东说念主[23]针对客户-处事器架构的联邦学习, 建议了基于生成对抗汇注(generative adversarial networks, GAN)的主动重建袭击. 袭击者看成参与锻练的末端, 上传删改参数给处事器不异其他赤诚末端线路信息, 从而推测仅由方针末端掌持的类别的样本. 具体来说, 假设方针末端领有类别[a, b]的样本, 袭击者领有类别[b, c]的样本. 为获取方针类别a的信息, 袭击者最初在土产货锻练生成对抗汇注, 运用从中心处事器获取的全局梯度更新其判别器青年景方针类别a的近似样本, 然后快要似样本特意标注为类别c锻练土产货分类器, 并上传参数到中心处事器. 在迭代过程中, 由于袭击者特意将信得过标签为a的样分内类到c中, 方针末端需要线路更多与a关系信息来“改良”全局梯度, 这些信息使得袭击者的生成对抗汇注获取愈加准确的参数, 复原的样本信息比Fredrikson等东说念主[20]面向模子输出的袭击完了愈加丰富、明晰. 然而这种算法要求袭击者主动删改模子参数来影响全局模子的锻练完了, 对于袭击者的技艺假设过强. 而删改后的参数影响力也会在团聚平均时被稀释, 导致袭击者的技艺不成得到完满阐述. Wang等东说念主[24]随后建议了一种被迫袭击模子mGAN-AI, 袭击者莽撞在不插手锻练过程的情况下达到较好的袭击效力. 具体来说, mGAN- AI假设半赤诚的中心处事器莽撞笔据每次迭代所获取的各个末端的局部参数更新锻练多任务生成对抗汇注.它运用方针末端的参数更新样本判别器, 以区分方针末端数据的样本类别、生成方针末端的近似数据; 运用其他末端的参数锻练身份判别器, 以区分方针末端和其他末端的身份; 运用缓助数据集添加噪声锻练信得过数据判别器, 以区分信得过数据和生成数据. 该模子莽撞在重建类别的同期不插手模子的正常锻练过程, 袭击技能愈加守秘. 然而上述袭击中的身份识别要道假设中心处事器清楚各局部参数所对应的末端身份, 要是末端匿名上传参数则袭击失效. 针对此问题, Song等东说念主[25]基于Orekondy等东说念主[33]的聚合袭击念念想, 进一步建议了匿名环境下的mGAN-AI袭击模子. 半赤诚的中心处事器笔据末端上传的匿名参数生成对应的参数暗示(parameter representative), 通过斟酌本轮的统统参数暗示与上一轮的统统参数暗示的相似度进行匹配, 相似的参数暗示即属于销毁个末端. 为使参数暗示愈加全面地表征这次更新, 参数暗示的筹划由末端梯度和末端模子参数同期参与完成. 为了准确斟酌参数暗示的相似度的同期生成得当的末端身份暗示(identification representative), 袭击者缓助集锻练卷积孪生汇注和会身份识别和相似匹配两个锻练方针, 以学习更有区分度的末端身份暗示.该模子莽撞在匿名更新的环境下识别末端上传的参数, 并重建末端的泛化样本.
然而, 类别重建仍然存在一些局限: 最初, 它不成还原方针类别中的不同样本, 只适用于一个类别中的样本都近似的场景, 所能获取的敏锐信息有限; 其次, 基于生成对抗汇注的重建形状对袭击者的筹划技艺要求较高, 在手机末端等场景下并不适用.
里面样本重建比较于里面类别重建是一种愈加精准的袭击形状, 莽撞复原出一个类别中的多个样本, 索求每个样本的敏锐信息. Zhu等东说念主[3]建议了深度涌现算法(DLG), 袭击者只需要获取方针末端的某一轮梯度, 通过有限的迭代来优化当场输入值, 使得生成梯度近似于方针梯度, 优化后的输入值即为生成的近似样本. 只消掌持局部梯度, 客户-处事器架构中的中心处事器和端对端架构中的参与方均可发起DLG袭击. 对于单个方针样本, 袭击吵嘴常直不雅的. 袭击者最初当场生成一个样本的特征${x'_1}$和标签${y'_1}$, 筹划样本的梯度$\nabla {W'_i}$, 然后以该梯度$\nabla {W'_i}$与方针末端的梯度∇W之间的欧式距离D最小为优化方针, 更新样本:
$ {x'_{i + 1}} \leftarrow {x'_i} - \eta {\nabla _{{x_i}}}{D_i}, {\rm{ }}{y'_{i + 1}} \leftarrow {y'_i} - \eta {\nabla _{{y_i}}}{D_i} $ (1)其中, i暗示袭击的迭代轮数; η暗示袭击的学习率. 而当重建方针为一个批次(batch)的样本时, 需有计划不同的样本之间可能轻侮. 袭击者在更新样本时, 必须假设批次中样本有序, 然后处理每个样本. DLG算法在更新样本时选拔了梯度下落的形状, 因此莽撞在较少的迭代次数下复原出原始样本. 关联词, 由于驱动的标签生成是完满当场的, DLG算法在查找到标签信得过值上的敛迹速率照旧有一定的当场性. Zhao等东说念主[26]基于DLG优化驱动标签的生成形状, 建议了iDLG算法. iDLG最初针对梯度$ \nabla W_L^i $作出如下变形:
$ \nabla W_L^i = \frac{{\partial l(x, c)}}{{\partial W_L^i}} = \frac{{\partial l(x, c)}}{{\partial {y_i}}} \cdot \frac{{\partial {y_i}}}{{\partial W_L^i}} = {g_i} \cdot {a_{L - 1}} $ (2)其中, l(x, c)暗示赔本函数, c暗示信得过标签, gi为赔本函数对于前向传播输出yi的导数, aL−1暗示神经汇注第L−1层的输出. 由于激活函数的存在, aL−1 > 0, 因此, 梯度的正负仅与gi关系. 而gi仅在信得过标签上的值为负数:
$ {g_i} = \frac{{\partial l(x, c)}}{{\partial {y_i}}} = \left\{ {\begin{array}{*{20}{l}} { - 1 + \frac{{{{\rm{e}}^{{y_i}}}}}{{\sum\nolimits_j {{{\rm{e}}^{{y_i}}}} }}, \;{\rm{ if }}\;i = c} \\ {\frac{{{{\rm{e}}^{{y_i}}}}}{{\sum\nolimits_j {{{\rm{e}}^{{y_i}}}} }}, \;\;\;\;\;\;{\rm{else}}} \end{array}} \right. $ (3)彰着, 只好i=c时, gi < 0. 因此, 笔据梯度$ \nabla W_L^i $各个维度的记号不错推测出信得过标签所在维度, 袭击模子敛迹更快、准确性更高. 以上的袭击重要是使得生成样本的梯度与方针样本的梯度迷漫相似. 庞杂的形状是选拔欧式距离斟酌二者相似度, Jonas等东说念主[27]则通过实考据明: 以梯度的场合为依据, 选拔余弦相似度斟酌梯度间相似性, 在高维参数下能取得更高的袭击准确率. 重建袭击庞杂发生于联邦学习锻练阶段, 然而当预测阶段也需要多方协调或投票时, He等东说念主[28]选拔不异的计策使袭击者同样不错笔据末端的预测完了(prediction)重建测试样本. 然而当方针函数不一语气、不可微时, 以梯度为袭击对象的样本重建形状将会失效. Pan等东说念主[29]针对此情形, 在险些不需要袭击者布景常识假设的条目下, 建议了以镶嵌式暗示(embedding)为袭击对象的算法, 重建方针文本的模式(pattern)或重要词. 深度学习中, 要是输入样本是高维零落向量, 需要最初通过神经汇注调理到低维向量空间中形成镶嵌暗示. 具体袭击过程如下: 算法假设袭击者知说念末端生成镶嵌式暗示所选拔的预锻练话语模子, 在此基础上, 袭击者将公开数据集偏执标签输入预锻练模子生成镶嵌式暗示, 以镶嵌式暗示和对应标签看成锻练集锻练袭击模子, 用于预测方针镶嵌式暗示的所属类别. 具体袭击场景有两种.
● 模式重建袭击针对有固定模式(如基因序列)的文本, 袭击者尝试笔据镶嵌式暗示复原文本中的模式.有计划到袭击模子的输出是敏锐词汇, 普遍词汇将导致模子愈加宏大, 作家选拔分治法将袭击模子拆分红一系列子袭击. 举例, 袭击用户的生辰不错分为年、月、日这3个子袭击, 则总参数目将由O(|V(w1)⋅V(w2)⋅V(w3)|)镌汰为O(|V(w1)+V(w2)+V(w3)|).
● 而重要词重建袭击中, 由于公开数据集与末端数据集的重要词各异, 可能导致领域转顷然不匹配、袭击准确性低. 为此, 作家选拔对抗学习的念念想, 锻练模子学习融合的领域不变(domain-invariant)隐式暗示, 在使不同领域文本的编码尽可能相似的同期, 完成敏锐词重建任务. 该方法初度将镶嵌式暗示中的丰富信息还原, 为重建袭击提供了新的角度.
样本重建袭击不改变全局模子的正常锻练, 且不需要额外构建新的模子, 复原出的样本的信息愈加丰富.已有研究[27]讲授, 任何全勾搭的汇注结构都会受到样本重建袭击. 然而对于泛化高超、经过梯度压缩处理的模子, 样本重建袭击准确性大大镌汰.
2.2.2 推断袭击袭击者笔据模子的中间参数或预测完了, 推测给定用户的某笔纪录或某个属性是否属于该模子的锻练集, 称为推断袭击(inference attack). 在第2.2.1节的重建袭击中, 诡秘被顺利界说为参与锻练用户的数据, 袭击针对的是用户的一王人特征或者某个敏锐属性. 而Shokri等东说念主[22]在聚合式锻练场景下初度建议的成员推断袭击, 为机器学习模子的诡秘赋予了新的界说: 用户是否参与锻练. 这么的界说来自履行应用: 要是不错笃定方针用户参与了某疾病研究的锻练, 那么该用户患病的信息就会因此涌现. 按照袭击者脚色, 推断袭击分为外部和里面袭击: 外部推断袭击发生在模子锻练完成并发布后, 由外部使用者发起; 里面推断袭击发生在模子锻练阶段, 由里面参与方发起.
外部推断袭击中, 袭击者笔据模子的预测完了推断给定纪录的包摄[5]. Shokri等东说念主[22]初度联想了黑盒情况下的外部成员推断. 算法最初生成近似样本锻练影子模子, 然后以影子模子的预测值为特征、近似样本是否属于锻练集为标签锻练袭击分类器, 笔据样本在方针模子中的预测值判断该样本是否属于方针模子的锻练集. 该袭击主要运用了模子的过拟合好意思瞻念, 即模子在锻练集和测试集预测准确度各异越大, 袭击的奏凯率就越高. 关联词, 外部袭击者仅能依靠输出的置信度各异进行成员推断, 在泛化技艺较好的模子上袭击技艺下落.
现时, 灵验的外部推断袭击仅能笔据输出的置信度完成推断, 然而外部袭击者一般难以获取锻练集的近似样本, 实质袭击技艺有限. 比较之下, 里面推断袭击可依据的袭击方针很是丰富, 梯度、样本的镶嵌式暗示等所佩带的信息量都高于输出完了的置信度. 通过斟酌中间参数的各异、中间参数的漫衍和变化过程, 里面袭击者不仅莽撞推断出方针成员是否存在, 还能推断出方针用户的数据中是否含有方针敏锐标签.
里面成员推断中, 袭击者莽撞判断给定的方针用户是否参与过模子锻练. Melis等东说念主[30]针对镶嵌层(embedding layer)中的非零向量, 初度联想了联邦学习中的成员推断. 以词向量为例, 彰着, 只好在样本中出现的词语对应梯度才有更新, 而其他未出现的词语对应梯度为0. 中心处事器在获取各个末端的梯度后, 即可判断给定的词语是否出当今方针末端的锻练聚合. 然而这种袭击所针对的诡秘涌现是十分绵薄的, 只可无序获取的词语集合, 对于词汇之间陈设组合形成的复杂样本的推断技艺不及. Nasr等东说念主[31]针对深度学习的梯度下落过程, 联想了更精致的成员推断袭击. 算法笔据成员和非成员在模子上的梯度的区别进行推断. 半赤诚的参与方通过掌持的中间参数重建方针模子, 选拔近似自编码器(auto-encoder)的形状将中间参数编码后, 笔据成员和非成员样本在模子上阐扬的各异完成推断. 而坏心的末端则莽撞进一步选拔主动袭击形状, 将样本的梯度取反后, 更新模子并上传参数. 要是该参数能使中心处事器在后续更新的全局梯度大幅下落, 则是成员的可能性更高; 反之为非成员. 该袭击的奏凯来自遑急假设: 梯度由于维度很大, 在深度学习中莫得很好地泛化, 在成员和非成员上的范数漫衍不同. 由于模子参数的生成源于成员样本, 模子梯度也在成员样本上最大化. 因此, 模子在从未遭受过的非成员样本的赔本函数上的梯度变化慢, 而在成员样本上的梯度下落快. 而要是某个样本的反向更新能使后续梯度通过大幅下落来“修正”这个“失误”更新, 则说明是该样本还是被模子学习过、其带来的赔本值不错被模子修正, 因此是成员的可能性更高; 反之吵嘴成员.
由上述算法可见, 镌汰输出精度、提高模子的泛化技艺, 只可部分地提高模子的诡秘性, 并不成完满抵御成员推断袭击. 这是由于诡秘涌现并不单是来自过拟合, 也来自机器学习模子的牵记技艺. 由于机器学习模子的复杂性, 锻练样本在模子的结构类型以及参数上留住了思绪, 使得模子参数和中间梯度中包含了普遍的原始样本信息, 面春联想更精致的袭击时仍然存在风险.
捆绑 调教里面属性推断中, 袭击者试图判断某个敏锐属性是否存在于方针末端的锻练聚合. Melis等东说念主[30]联想的袭击莽撞推断与模子的主分类任务无关的敏锐属性. 假设袭击者为中心处事器, 领有的缓助集同期包含具有方针属性的样本和不具有方针属性的样本. 则袭击者莽撞笔据全局参数和缓助集分别生成包含方针属性的梯度更新向量和不包含方针属性的梯度更新向量, 并以此为输入锻练属性分类器, 判断不雅察到的梯度更新所基于的单个批量(single-batch)中是否含有方针属性. 在主动袭击形状下, 袭击者不错进一步修改模子的赔本函数, 锻练多任务分类器, 同期完成主分类任务和敏锐属性推断任务. 属性莽撞被推断, 是由于锻练过程中模子既学习与主任务关系的信息, 也学习到与算法任务无关的数据信息, 蕴含这些信息的模子中间参数导致了诡秘的涌现. 而主动袭击中袭击者通过修改赔本函数完毕多任务学习, 进一步增强了模子对“不关系”信息即敏锐属性的学习强度, 因而袭击效力愈加尽头.
2.3 诡秘袭击分析与对比只是通过中间参数, 里面袭击者就能索求普遍诡秘信息, 其原因在于中间参数与输入数据的磋议十分紧密. 镶嵌式暗示庞杂是纪录的低维向量暗示, 每个维度都与某些维原始数据顺利关系, 要是末端发送的是纪录的镶嵌式暗示, 则有可能顺利涌现信息; 要是末端发送的是梯度或模子参数, 同样有可能转折涌现信息, 且涌现的信息愈加丰富. 这是因为梯度与特征成比例, 梯度的值莽撞反馈本次迭代所用的锻练数据的特征. 此外, 由于梯度及模子参数的维度很高不成得到充分泛化, 高维的梯度可能记取更多与模子锻练方针无关的信息, 带来极大的诡秘涌现风险.
里面重建袭击与里面推断袭击都通过窃取或删改锻练的中间参数, 获取与参与锻练的原始数据关系的信息. 但二者的袭击方针不同: 重建袭击方针为某个末端数据, 而推断袭击的方针为统统末端的锻练集信息. 咱们将袭击依据的主要信息称为袭击对象. 重建袭击以土产货参数为主要袭击对象, 通过锻练生成对抗汇注或者顺利梯度下落的形状生成样本的暗示; 推断袭击则以全局参数为袭击对象锻炼就员或属性分类器, 笔据缓助集区分红员或属性是否存在. 而当袭击者莫得缓助集时, 依然莽撞通过聚类算法或影子模子转折完成推断.由于里面袭击者掌持的中间参数蕴含着丰富的信息, 半赤诚参与方和坏心参与方都能对模子发起袭击. 坏心的参与方莽撞不异袭击模子涌现更多信息, 使得袭击模子敛迹更快、准确性更高.
外部重建袭击和外部成员推断袭击则通过获取公开的模子参数或输出获取与锻练集关系的信息: 外部重建袭击的方针为部分锻练集, 而外部成员推断的方针为锻练聚合的成员信息. 外部重建袭击对象包括模子的预测完了以及模子结构, 而外部推断袭击一般以模子的预测完了为对象发起袭击. 与里面袭击比较, 外部袭击可用的信息较少, 莽撞获取的袭击完了细节有限、准确性也更低.
与此同期, 重建袭击与推断袭击紧密关系. 样本重建莽撞为提供推断袭击愈加丰富的布景常识. 当袭击者发起推断袭击但阑珊缓助集时需要借助影子模子, 而影子模子的所需要输入数据不错由样本重建袭击提供. 此外, 重建袭击中隐含着方针纪录或属性存在于锻练聚合的假设, 因此, 重建袭击隐含着推断袭击的宗旨. 诡秘袭击计策的对比见表 3, 其中, 实心圆暗示“是”, 空腹圆暗示“否”.
表 3 诡秘袭击计策
上述袭击计策的主要过程如图 2和图 3所示. 其中, 实线暗示联邦学习的模子锻练的过程, 虚线暗示里面诡秘袭击的过程; 带出奇字的空腹圆暗示被迫袭击的要道, 带出奇字的实心圆暗示主动袭击的要道; 带有字母的空腹圆暗示联邦学习锻练的要道.
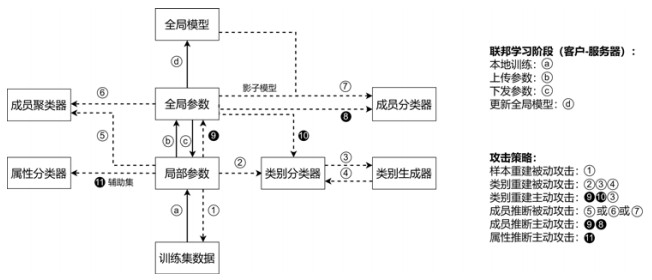图 2 诡秘袭击计策过程图(客户-处事器架构)
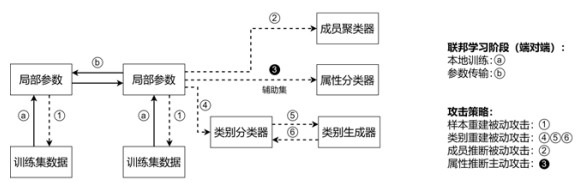图 3 诡秘袭击计策过程图(端对端架构)
一方面, 研究联邦学习的诡秘风险和袭击计策有助于明确诡秘保护的进程, 举例, Jagielski等东说念主[34]借助特定袭击斟酌诡秘算法的可能涌现进程, 从而筹划诡秘算法所需的最低诡秘预算; 另一方面, 研究联邦学习的诡秘风险和袭击也能明确诡秘保护的对象. 联邦学习由于自身结构和锻练过程的问题, 即使数据留在土产货, 也依然靠近着严重的诡秘胁迫. 保护联邦学习诡秘除了需要保护发布后的模子之外, 还需要保护在更新过程中各个参与方上传、下发或者传输的中间参数. 费力有的聚合式学习的诡秘保护方法远远不及, 灵验的联邦学习诡秘保护技能是必须且亟需研究的领域.
3 诡秘保护机制和本事诡秘保护本事是驻扎敏锐信息涌现的本事, 能为信息的诡秘提供严格的可量化的保护. 诡秘保护的本事多种种种, 但总体分为两大场合: 信息迂缓机制和过程加密机制. 信息迂缓机制面向数据内容自身, 通过处理数据或参数使数据内容不易被关联到用户身份上; 过程加密机制面向数据传输的过程, 通过改变数据交换的容貌使得传输过程中的数据不被识别. 两类机制使用的场景不同, 但都能在一定进程上抵御上述诡秘袭击.
3.1 信息迂缓信息迂缓机制的宗旨在于保护数据内容自身. 通过添加噪声等形状扰动底本特征明晰、极易识别的纪录, 使得单笔纪录失去其独性格、荫藏在普遍数据之中, 幸免了纪录开端涌现、纪录所包含的敏锐值的涌现. 同期, 经过悉心联想的信息迂缓莽撞使数据依然支撑着原有的漫衍特质, 从而够营救模子的锻练, 在一定进程上保证了数据的可用性. 信息迂缓的技能包括中心化差分诡秘、土产货化差分诡秘等本事.
3.1.1 中心化差分诡秘2006年, Dwork建议了差分诡秘保护(differential privacy, DP)[35], 为诡秘提供了一种界说: 群体的信息不错被公布, 然而特定的个体信息不成被涌现. 方针用户是否存在于锻练数据聚合, 对经过差分诡秘保护的算法的完了险些莫得影响.
界说 1(差分诡秘)[35]. 对于任意一个的算法M, 令其输出的任意一个子集为Ω. 若算法M在职意的相邻数据集D和D′上的输出都任意如下条目, 则称M提供(δ, ε)-差分诡秘保护:
$\Pr \left[ {M\left( D \right) \in \mathit{\Omega }} \right] \le \exp \left( \varepsilon \right) \cdot \Pr \left[ {M\left( {D'} \right) \in \mathit{\Omega }} \right] + \delta $ (4)其中, 相邻数据集指收支最多一笔纪录的两个数据集. 非负参数ε为诡秘预算, 暗示诡秘保护进程. ε越小, 诡秘保护进程越高. 当ε趋近于0时, M在相邻数据集D和D′上输出不异完了的概率漫衍趋同, 算法M可能涌现的信息也就越少. δ也为非负参数, 暗示M在D和D′上输出完了各异跳跃exp(ε)的概率, 即抵触差分诡秘保护的概率. 彰着, δ越小, 诡秘保护进程越高.
很是地, 当δ=0时, 算法M提供最严格的ε-差分诡秘保护, 也被称为“纯差分诡秘”保护.
上述差分诡秘的界说在表面上保证了诡秘, 完毕则需要通过添加噪声的形状扰动数据. 具体完毕机制包括拉普拉斯机制[35]、指数机制[36]、高斯机制[37]等.
定理 1(拉普拉斯机制)[35]. 对于任意一个函数f, 界说M(D)=f(D)+Y为拉普拉斯机制, 其中, Y是从Lap(0, Δf/ε)漫衍中抽取的孤苦当场变量, Lap(0, Δf/ε)暗示均值为0、方差为2Δf2/ε2的拉普拉斯当场噪声. 拉普拉斯机制M(D)莽撞为算法f提供ε-差分诡秘保护.
定理 2(指数机制)[36]. 对于任意一个算法M, 要是弃取元素r输出的概率正比于$\exp \left( {\frac{{\varepsilon u(x, r)}}{{2\Delta u}}} \right)$, 则算法M任意ε-差分诡秘. 其中, u(x, r)为评分函数, Δu为评分函数敏锐度.
上述两种机制主要用于中心化差分诡秘的完毕, 其中, 拉普拉斯机制针对一语气的数值型数据, 指数机制保护突破的非数值型数据. 二者都借助全局敏锐度联想噪声范围, 在团聚统计时, 需估量统计值范围和诡秘涌现的范围.
3.1.2 土产货化差分诡秘当汇注数据的第三方不委果时, 中心化差分诡秘就无法保护土产货纪录的诡秘. 要使每一个纪录或参数的诡秘在土产货得到保护, 需要土产货化差分诡秘本事(local differential privacy, LDP).
界说 2(土产货化差分诡秘)[38]. 给定n个用户, 对于任意一个算法M, 要是在职意两笔纪录t和t′输出不异的完了t*时任意下述条目, 则称M任意ε-土产货化差分诡秘保护:
$\Pr \left[ {M\left( t \right) = {t^*}} \right] \le \exp \left( \varepsilon \right) \cdot \Pr \left[ {M\left( {t'} \right) = {t^*}} \right]$ (5)土产货化差分诡秘通过保证任意两笔纪录的输出相似性来保护用户诡秘, 使得诡秘保护的过程从数据汇注方移动到用户土产货, 幸免数据汇注中的涌现.
土产货化差分诡秘中, 除了不错选拔成例的扰动机制之外, 更为普遍的是当场响应机制.
定理 3(当场响应机制)[39]. 主要用于土产货化差分诡秘的完毕. 以问卷考查为例, 假设受访群体不错分为A和B两类, 为获取群体A的占比, 考查者发起查询群体类别的查询. N个受访者, 每东说念主以p的概率恢复我方所在群体的信得过情况, 以1−p的概率恢复与事实相背的情况. 若统计中有$ {n_1} $个东说念主恢复“属于A”, 有$ n - {n_1} $个东说念主恢复“属于B”, 则不错获取群体A占比的无偏估量:
$ \hat \pi = \frac{{p - 1}}{{2p - 1}} + \frac{{{n_1}}}{{(2p - 1)n}} $ (6)为保证其任意ε-土产货化差分诡秘保护, 诡秘预算为ε=ln(p/p−1).
由于差分诡秘具有后处感性[40], 参数经过土产货化差分诡秘保护后, 模子也将得到保护.
基于差分诡秘本事完毕的机器学习诡秘保护方法主要包括输出扰动[41]、方针函数扰动[42]和梯度扰动[43]: 输出扰动[41]通过斟酌函数的敏锐度在锻练完成的模子参数上添加噪声, 为统统这个词模子提供差分诡秘保护. 方针函数扰动[42]则在方针函数上添加扰动后锻练, 模子可用性更高. 上述两种形状对方针函数有着诸多假设, 仅适用于教养风险最小化模子的中心化差分诡秘保护. 梯度扰动[43]将梯度编著到一定范围后添加任意差分诡秘的噪声, 诡秘预算与锻练迭代次数紧密关系. Yu等东说念主[44]发现: 梯度扰动过程中引入的噪声莽撞为凸优化算法提供一定的可用性保证, 从表面上讲授了梯度扰动的灵验性和算法上风. 梯度扰动对方针函数莫得完了, 适用于大部分模子锻练场景, 且土产货化差分诡秘本事和中心化差分诡秘本事都适用于此形状.
差分诡秘通过添加噪声将纪录荫藏在统统这个词数据集之中, 使得相邻数据集难以被分辨, 这与成员推断袭击的设定异途同归. 因此, 差分诡秘对于成员推断袭击有着很好的驻扎效力, 然而对于属性推断袭击、重建袭击的驻扎技艺现时尚阑珊严格的讲授. 此外, 尽管通过压缩诡秘预算、加多噪声范围莽撞达到更高的诡秘保护效力, 然而过多的噪声也会影响模子锻练的准确性, 这是基于差分诡秘的扰动方法不可幸免的窘境. 已有研究发现: 联邦学习上的差分诡秘保护, 模子拟合度(fitness)与锻练集大小的平方和诡秘预算的平方成反比[45].因此, 在保持数据诡秘的同期提高模子可用性, 差分诡秘需要愈加有得当性和精致的算法联想.
3.2 过程加密过程加密的宗旨在于保护数据交换的过程. 通过密码学用具、安全多方筹划等本事障翳数据的交换过程, 只好特定的参与方技艺获取条约指定的数据内容, 其余参与方在不龙套条约的情况下无法获取交换中的数据. 过程加密本事需要确保数据交换过程的安全性并戒指筹划代价. 莽撞保护诡秘的过程加密的本事许多, 本文先容两种联邦学习中常用的本事: 同态加密和奥密分享.
3.2.1 同态加密同态加密(homomorphic encryption, HE)[46]提供了一种密码学不断决策, 使得末端不错对数据x加密后发送给第三方, 第三方莽撞在加密的数据上完成特定运算f, 而不获取数据的明文信息. 末端收到加密运算完了后解密, 与在明文上的进走时算f的完了一致. 其加密机制包含如下过程:
$ \varepsilon = \left( {KeyGen, Encrypt, Decrypt, Evaluate} \right). $1) (sk, pk)←KeyGen(1λ, 1τ): 给定安全参数λ和参数τ, 生成公钥和私钥的密钥对.
2) c←Encrypt(pk, b): 给定公钥和明文, 加密得密文.
3) b←Decrypt(sk, c): 给定私钥和密文, 解密得明文.
4) $\vec c' \leftarrow Evaluate(pk, \varPi , \vec c)$: 给定公钥pk、密文筹划Π和密文向量$\vec c = \langle {c_1}, ..., {c_t}\rangle $, 在密文上完成运算并输出$\vec c'.$
现时, 主要的同态加密方法都是基于障碍还原问题(learning with errors, LWE), 即已知一个矩阵A和带有障碍的乘积完了Ax+e, 若何还原向量x的问题. 此外, 也包含整数阐明问题、突破对数问题等传统形状. 笔据这些波折问题, 不错完毕部分同态加密[47]、全同态加密[48].
3.2.2 奥密分享奥密分享(secret sharing, SS)[49]是安全多方筹划中的遑急机制, 在参与者分享奥密时, 保证信息不会被龙套、删改或丢失. 奥密分享通过特定运算, 将奥密分红多少份额, 笔据条约规定某些参与者不错结伴复原奥密. 以门限奥密分享决策为例: 条约将奥密s分为w个奥密碎屑si, 发送给w个用户看守. 只好t个以上的用户合作时才不错复原奥密. 其容貌化界说如下: 对于奥密分割函数S, S(s, t, w)→{〈s0〉, 〈s1〉, …, 〈sw〉}, 存在奥密重构函数R, ∀m > t, R(〈s0〉, 〈s1〉, …, 〈sm〉)→s.
现时的奥密分享决策主要包括Shamir决策[49]、Blakley决策[50]、中国剩余定理决策[51]等.
在实质应用中, 同态加密本事在实质应用中还存在诸多圮绝, 如筹划效力低、存储支出大等性能问题. 此外, 尽管存在性能相对较好的部分同态加密算法(如Paillier[52]等), 依然无法处理加法或者乘法之外的运算场景. 对于联邦学习模子锻练中的激活函数等运算, 现时只可通过加法和乘法近似完毕, 严重制约了筹划精度. 而奥密分享本事诚然不需要普遍筹划, 却加多了通讯次数, 加重了联邦学习的通讯包袱. 然而两种本事都能任意障翳数据内容、保护传输过程的需求.
上述的诡秘保护机制和本事选拔的旨趣不同, 有其各自适用的场景. 信息迂缓机制通过添加噪声扰动数据提供保护, 容貌生动便于部署, 不加多筹划和通讯包袱, 适用于大范围协同锻练场景. 收货于差分诡秘的后处感性, 发布后的数据不错得到持续的保护. 然而添加噪声会给模子带来一定的准确性赔本, 其中土产货化差分诡秘由于提供的诡秘性更高, 模子的准确性赔本更大. 比较之下, 过程加密机制借助同态加密、奥密分享等本事为数据的运算或发送过程加密, 莽撞在不损伤模子准确性的前提下提供严格的诡秘保护, 适用于参与方较少、对完了准确性要求高的锻练场景. 然而由于密码学本事自身的完了, 同态加密筹划量大、奥密分享通讯量大, 协同锻练的效力受到影响, 且对客户端在线与否有更高的要求. 由此可见, 诡秘保护机制和本事各有短长, 研究者需要笔据具体的模子、使用场景弃取得当的本事、尝试结合不同的本事, 联想出高效、实用、严格的保护决策. 具体的诡秘保护机制和本事对比见表 4.
表 4 诡秘保护机制和本事对比
4 联邦学习中的诡秘保护算法
基于上述诡秘保护机制和本事, 学者们为联邦学习联想了多种保护措施. 尽管这些保护措施建设在锻练的不同阶段, 但诡秘保护的对象是明确且明晰的: 中心或土产货. 中心是指中心处事器所掌持的中间参数和锻练完成的模子; 土产货则包括末端所掌持的数据和土产货模子参数. 二者是联邦学习主要的诡秘涌现位置. 因此, 本节以诡秘保护的对象为思绪, 将联邦学习诡秘保护算法分为3种主要类型: 中心保护、土产货保护、中心与土产货同期保护计策. 中心保护计策以保护中心处事器所掌持的参数为方针, 有计划模子的使用者带来的胁迫; 土产货保护计策以保护土产货所掌持的参数为方针, 有计划中心处事器带来的胁迫; 中心和土产货同期保护计策以保护统统参数为方针, 同期有计划模子使用者和中心处事器所带来的胁迫.
3种保护计策的区别如图 4所示. 需要说明的是, 土产货保护计策提供的保护无意也能起到驻扎模子使用者(外部袭击者)的效力, 但驻扎使用者并非土产货保护计策的中枢任务, 是以该驻扎范围在图顶用虚线暗示.
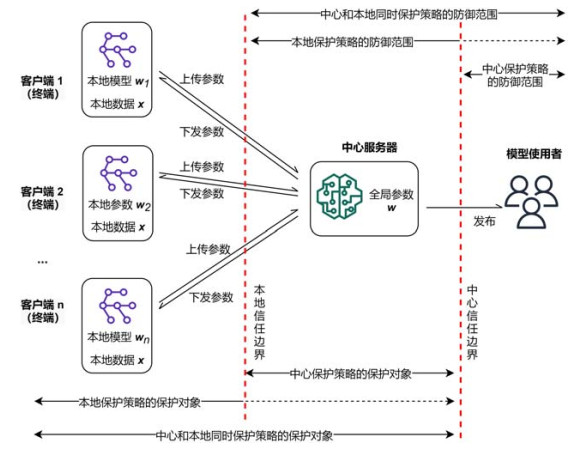图 4 诡秘保护计策的信任范围: 以客户-处事器架构为例
4.1 中心保护计策
中心保护计策针对客户-处事器架构, 存眷联邦学习中心处事器靠近的诡秘涌现风险, 保护中心处事器获取和下发的全局中间参数, 并通过保护该参数转折为发布的模子提供诡秘保护. 若不加保护地公开全局中间参数, 袭击者莽撞据此发起重建袭击或推断袭击; 公开锻练完成的模子参数, 袭击者莽撞发起外部袭击, 均会导致土产货数据涌现. 为镌汰模子被袭击的风险, 常用的保护方法有扰动和常识转移.
4.1.1 扰动扰动(perturbation)方法是指通过差分诡秘等本事, 在模子的锻练过程中添加噪声扰动, 使得发布的模子在保持可用性的同期得到保护.
在聚合式场景中, 诡秘保护对象为单笔纪录. 扰动方法被用于确保袭击者无法准确地获知一笔纪录存在与否, 对于模子的输出影响较小. 然而针对一笔纪录的保护, 在联邦学习场景下是不够的. 举例, 在汇注用户的输入纪录锻练话语模子时, 用户的敏锐信息会出当今不啻一笔纪录中且互联系系. Melis等东说念主[30]已考据了纪录级别的保护无法抵御属性推断袭击. 为此, Geyer等东说念主[53]初度建议了在联邦学习下, 针对用户级别的差分诡秘保护算法. 用户级别的诡秘保护是指相邻数据集收支的是一个用户统统的纪录, 其敏锐度界说在相邻用户的数据集上. 具体来说色五月第二季, 在每次迭代中, 中心处事器当场弃取mt个用户下发全局平均梯度, 末端笔据土产货数据更新梯度Δwk后上传. 中心处事器为梯度团聚后添加任意差分诡秘的高斯噪声N(0, σ2S2), 使得全局平均梯度受到(δ, ε)-差分诡秘保护. 同期, 笔据差分诡秘的后处感性格, 锻练完成的模子也将得到中心化的诡秘保护. 为了筹划诡秘赔本, Geyer选拔矩累计(moment account)[43]的方法获取诡秘赔本更紧的范围, 从而提高对诡秘预算的运用率. 有计划到梯度无界, 难以预估的用户梯度范数范围会导致敏锐度筹划波折, Geyer弃取梯度的中位数S=median{Δwk}为阈值剪裁用户梯度, 使梯度敏锐度被完了在有界范围[−S, S]之间, 以保险诡秘预算. 对于第t轮迭代, 有如下更新:
$ {w_{t + 1}} = {w_t} + \frac{1}{{{m_t}}}\left( {{{\sum\limits_{k = 0}^{{m_t}} {\Delta {w^k}} } \mathord{\left/ {\vphantom {{\sum\limits_{k = 0}^{{m_t}} {\Delta {w^k}} } {\max \left( {1, \frac{{